|
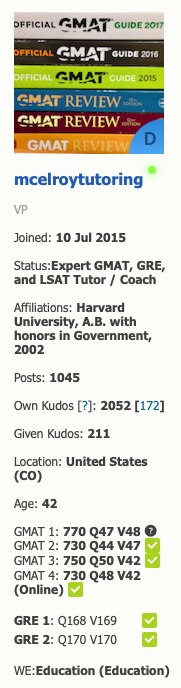
old GMAT Club profile page, circa 2022
Did you know that GMAT Club is a helpful resource for free GMAT preparation? I have maintained an active profile on the site since 2015, with over 1,200 posts and 2,500 "kudos" earned as of July 2025.
Unlike many other well-known GMAT tutors who claim high scores but offer zero proof, I have also utilized GMAT Club's proprietary score verification system (green checkmarks above) to verify my own GMAT subscores of Q50 / V47, as well as my perfect score of 340 on the GRE.
I also continue to post and comment occasionally on other social-media websites such as Reddit, using anonymous and alternate / burner accounts — my original "SkypeTutor" account with over 75,000 karma and 300 Reddit awards was suspended in 2021, due to false reports filed by envious employees of competing test-prep companies, including the moderators of other popular test-prep subreddits.
Below are some of my greatest hits on Reddit's r/GMAT and r/GRE from back in the SkypeTutor days:
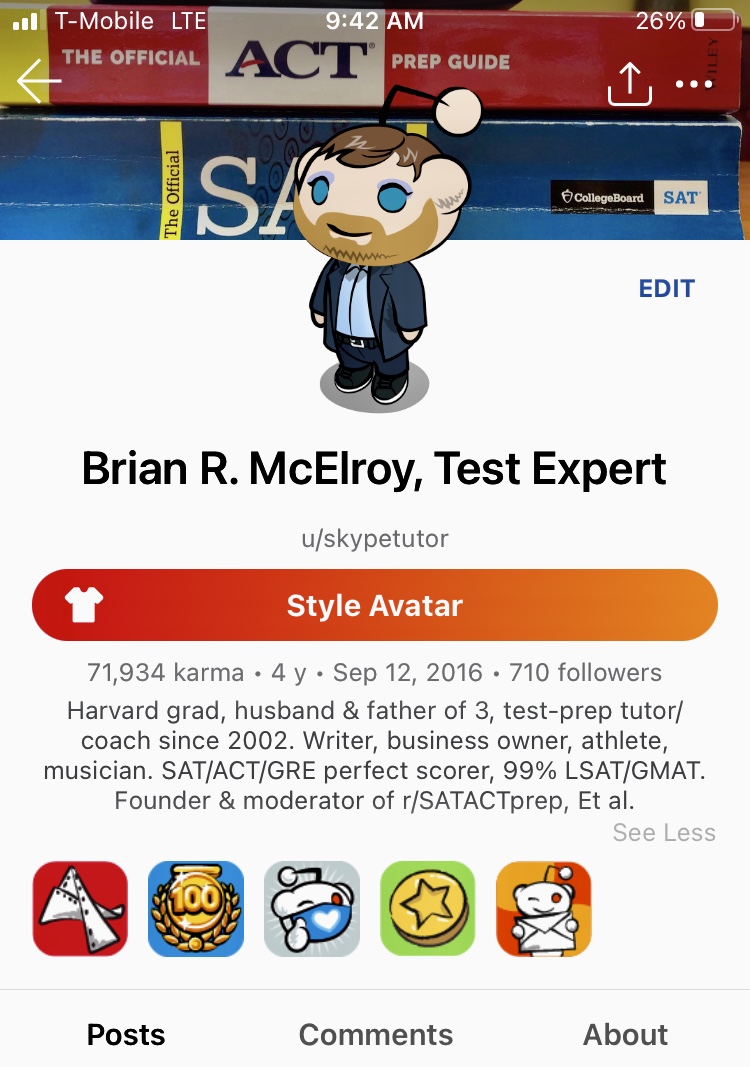
I'm a 40 year-old Harvard grad & professional GMAT tutor. I graduated college in 2002, but didn't start taking the GMAT until 2012. Since then I have taken the GMAT 6 times and scored 700, 710, 730, 730, 750 and 770. AMA.
Hi, I'm Brian R. McElroy aka SkypeTutor: test-prep expert, professional GRE tutor since 2002, verified perfect 340 GRE scorer (6/6 AWA), 99% LSAT (179) and GMAT (770) scorer, co-author of *GRE Vocab Capacity* & *Vince and Brian's Free GRE PowerPrep Explanations*, & Harvard graduate with honors. AMA.
From 770 to 710 to 730 to 700 to 750: I've taken the GMAT 5 times and scored in the 700s every time. AMA.
I'm Brian R. McElroy. Harvard grad (class of '02), 770 GMAT Scorer and Professional GMAT Tutor Since 2002. AMA.
The New, 23-Minute Shorter GMAT Debuts Tomorrow. Here are the Details.
And here are some of my most popular GMAT Club posts:
*From 680 to 770 in 6 Weeks (*a GMAT Club "debrief" written by a former private tutoring student)
Someone tried to steal my GMAT score...and got caught by GMAC.
PSA: the scoring on the real GMAT is different from that of GMATPrep.
A GMAT Tutor's Guide to the Official Guide for GMAT Review 2021
GMAT Quant + Verbal Composite Score Conversions and Percentiles 2020
GMAC Finally Updated its GMAT Percentile Rankings for 2019
An Introduction to GMAT Critical Reasoning by Brian McElroy
From Q42 to Q44 to Q46 to Q50: my GMAT Quant Journey (with ESRs)
From V46 to V47 to V40 to V42: my GMAT Verbal Journey (with ESRs)
I scored a 750 on the GMAT (with the new "Select Section Order" feature)
GMAT Pacing Strategy: The 20/30 Method
7 Important Questions to Ask Your Prospective GMAT Tutor.
Use the GRE Score Comparison Tool for B-Schools to compare GRE & GMAT Scores
How to get 12 Questions Wrong on the GMAT and still earn a Perfect 800
GMAT Test-Day Tips From a Harvard Grad and 770 Scorer
Sample AWA Prompt and 6/6 Essay
GMAC Announces a Lifetime Limit of 8 GMAT Exams (spoiler alert: the lifetime limit has now been removed)
My Review of the 2017 GMAT Official Guide
Why Diagnostic Exams are Overrated for High Scorers (and most others)
Why You Should Use Only Real GMAT Questions
Leveraging the GMAT Scoring Algorithm to Your Advantage
The Benefits and Limitations of GMAT Question Classification
Realistic GMAT Score Improvements
How to Use Keyboard Shortcuts to Auto-Save GMAT Question Screenshots (for Windows and Mac)
How to Access All 1,500 Questions from Your Free GMATPrep Tests
How to Score Q47 by Concentrating on the First 25 Questions (with ESR)
How to Get Instant Feedback on OG Questions Using The Free Wiley QB
11 Helpful Math Formulas for GMAT Quant
Time-Saving Keyboard Shortcuts for GMATPrep tests & the Real GMAT Exam
Read my full profile (registration required): http://gmatclub.com/forum/members/member-526882.html
Finally, you also find my profile on Amazon, where I have been one of the world's top customer reviewers of test-prep guides for the last 20 years.
Though I am now retired from writing customer reviews, you can still peruse my opinions on the 2023-2024 GMAT Official Guide Bundle and the 2024-2025 GMAT Official Guide Bundle, among other popular GMAT books.
-Brian
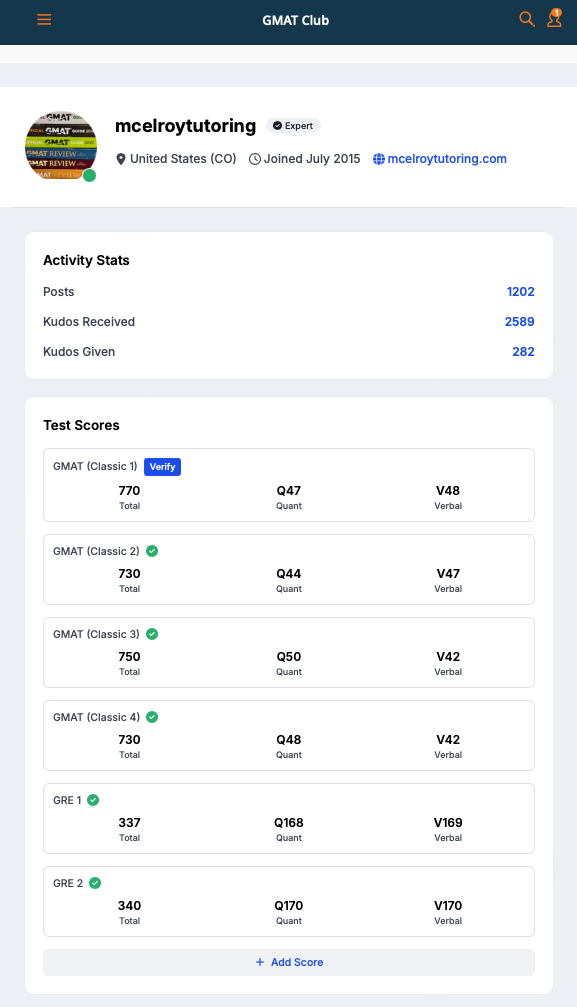
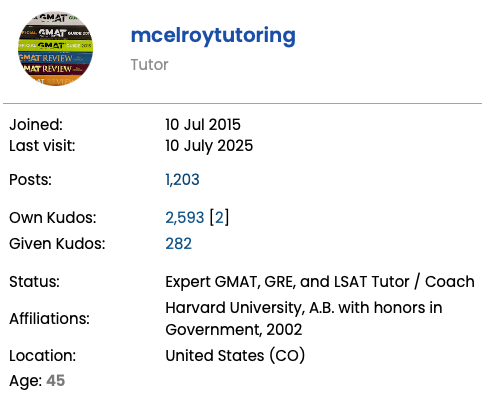
new GMAT Club profile page, 2025 (10 years and counting!)
Back to Blog Home
| 





